AVL tree insertion!!!

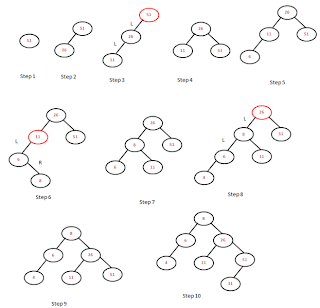
Lets constrcut the AVL tree with numbers 51, 26, 11, 6, 8, 4, 31, 21, 9, 16.  AVL tree is a balanced Binary search tree. So to construct AVL tree, we need to follow below steps

• insert the new element in such a way that if the element is less than the current node go left and if the element is greater than go right.
• Check for the balance at each node after insertion (diff between left subtree and right subtree should be atmost one)

we will see step by step after inserting each number into the tree from starting. The numbers are
 51, 26, 11, 6, 8, 4, 31, 21, 9, 16.

• In step1 the tree is empty , so 51 is the first node, in step2 26 is inserted as a left child to the root node 51 and the tree is balanced.
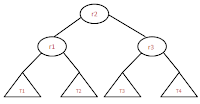
• In step3 11 is added as a left child to the node 26, becaus of this root node 51 is un-balanced, as it is shown in the image as red circle. We need to do the left left rotation which is a single rotation.
• After the rotation, tree is balanced as shown in step4.
• in step5 we are inserting 6 into the tree and which is as a left child to the node value 11.
• in step6 we are inserting 8 into the tree and which is as a right child to the node value 6, because of this tree is un-balanced at node value 11 which is marked as red circle in the image.
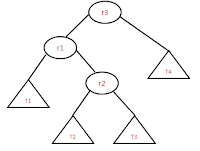
• for balancing the node we need to do right-left rotation which is a double rotation.
• After the rotation, the tree is balanced and it is like as shown in step7.

• In step8 we are inserting 4 into the tree and which is as a left child to node value 6. Becaus of this insertion, the tree is un-balanced at node value 26, and we need to do the left-left rotation as we did it earlier.
• After the rotation the tree is like shown in step9. After that we need to insert 31 into the tree and which is as a left child to the node value 51 as shown in step10. And the tree is balanced.
• In step11 we are inserted 21 into the tree whihc is as a right child to the node value 11. In step12 we inserted 9 as a left child to the node value 11. And the tree is balanced.
• in step13, becaus of inserting 16 as a left child to the node value 21, the tree is un-balanced at node value 8.

• We need to do the left right rotation  which is a double rotation. And the resultant tree is as shown in step14.

AVL tree double rotation!!

Double rotation: need to do two rotations (left-right or right-left) to balance the tree. In this there are two types of sub rotations

• Right Left rotation
• Left Right rotation



Before Rotation

 Right-Left rotation:  This is double rotation method in which we need to do two rotatios left and right. And this method needs to apply if the tree is as shown in the below image.

• Here r3 is un balanced and we need to do RL rotation because r2 is right child of r1 and r1 is left child of un balanced r3.

• Rotation is done in such a way that T1<r1<T2<r2<T3<r3<T4 property should satisfy after rotation.



After Rotation

• To balance the tree, make r2 as root node and follow the binary search tree property for all other nodes.
• Sample C code for Right Left rotation is given below. 

      
      //below steps are making the tree as shown in the image before rotation
      r1 = r3-<left;
      r2 = r1-<right;
      t2 = r2-<left;
      t3 = r2-<right;
  
      // actaul rotatiosn happens here
      r1-<right = t2;
      r3-<left = t3;
      r2-<left = r1;
      r2-<right = r3;
  
      //updte the new heihts for r1, r2, r3
      set_height(r1);
      set_height(r2);
      set_height(r3);
  
      *r = r2;
  
  

Left Right rotation: This is double rotation method in which we need to do two rotatios right and left. And this method needs to apply if the tree is as shown in the below image.





Before Rotation


• Here r1 is un balanced and we need to do RL rotation because r2 is left child of r3 and r3 is right child of un balanced r1.
• Rotation is done in such a way that T1<r1<T2<r2<T3<r3<T4 property should satisfy after rotation.



After Rotation

• To balance the tree, make r2 as root node and follow the binary search tree property for all other nodes.
• Sample C code for Right Left rotation is given below.

      //below steps are making the tree as shown in the image before rotation
      r3 = r1-<right;
      r2 = r3-<left;
      t2 = r2-<left;
      t3 = r2-<right;
  
      // actaul rotatiosn happens here
      r1-<right = t2;
      r3-<left = t3;
      r2-<left = r1;
      r2-<right = r3;
  
      //updte the new heihts for r1, r2, r3
      set_height(r1);
      set_height(r2);
      set_height(r3);
  
      *r = r2;
  
  

AVL tree Single rotation!!

Single rotation: As the name says need to do one rotation (left or right) to balance the tree. In this there are two types of sub rotations

• Left left rotation
• Right right rotation

 Left Left rotation: This is single rotation method which needs only one rotation. Left-Left rotation is required if the un-balanced tree is like as shown in the image.


Before Rotation

• Here r2  is un-balanced, because of adding the new node at T1 sub tree. Newly added node could either left or right. But it changes the balance property of r2.
• To balance the tree, we need to do left-left rotation. This is because of newly added node is left child of r1 and r1 is a left child of un-balanced node r2.
• Rotation is done in such a way that T1<r1<T2<r2<T3 property should satisfy after the rotation also.

• 

  After Rotation

  After the rotation the tree would be as shown in the image.
• To make the tree balance, make the r2 as the root, and follow the Binary search tree property after that, we will get the resulted tree.
• Sample code to do left-left rotation

  r1 = r2->left;
  //we are @r2, below statements are to make the tree like
  // shown in the image. so that rotation becomes easy
  t1 = r1->left;
  t2 = r1->right;
  t3 = r2->right;
  
  //actual rotation happens here
  r1->right = r2;
  r2->left = t2;
  
  // update the r1 , r2 height
  set_height(r1);
  set_height(r2);
  

Right Right rotation: This is single rotation method which needs only one rotation. Right-Right rotation is required if the un-balanced tree is like as shown in the image.





Before Rotation


• Here r1 is un-balanced, because of adding new node to the subtree T3 either left or right. But it changes the balanced property of r1.
• We need to do right-right rotation because newly addded node is right side of r2, and r2 is right side of the unbalanced node r1.
• Rotation is done in such a way that T1<r1<T2<r2<T3 property should satisfy after the rotation also.



After Rotation

• After the rotation, resulted tree shouls be as shown in the image.
• To make the tree balance, make the r2 as the root, and follow the Binary search tree property after that, we will get the resulted tree.
• See the sample code for right-right rotation below.

      
      //we are @r1 and below statements are
      // used to arrange the pointers looks like in the image
      r2 = r1-<right;
      t1 = r1-<left;
      t2 = r2-<left;
      t3 = r2-<right;
  
      // actual rotations happens here
      r1-<right = t2;
      r2-<left = r1;
  
      set_height(r1);
      set_height(r2);
  
      *r = r2;
  
  

AVL tree rotation!!!

AVL tree is balanced binary search tree. When we try to add new node to the AVL tree, it may become un-balanced. Generally the node which is unbalanced is grand parent of the newly inserted node. To balance the AVL tree, we need to do rotations. There are two types of rotations.

• Single rotation: As the name says need to do one rotation (left or right) to balance the tree. In this there are two types of sub rotations
• Left left rotation
• Right right rotation

• Double rotation: need to do two rotations (left-right or right-left) to balance the tree. In this there are two types of sub rotations
• Right Left rotation
• Left Right rotation

pthread_mutex_lock(&mutex_)failed with error 22!!

Recently I came across below problem while I was writing the gmock test for our source code. gmock is a unit test framework for C++. gmock is short form of Google Mocking.

gtest/internal/gtest-port.h:1151:: pthread_mutex_lock(&mutex_)failed with error 22
Abort

 

I got the above error two times while I was writing UT test cases. See the two scenarios below.  

1. Extra EXPECT_CALL :  This could be one of the reasons for the above problem. In my test case I have lot of EXPECT_CALL's, because our function is calling lot of other functions, so I need to mock all the functions, in the process of mocking these functions, by mistake I mocked one function which is not been called by this function. That means I added one extra EXPECT_CALL.  By taking stack trace using GDB I found the function and commented that expect call. And it was working fine.  
2. Used Once instead of Repeatedly: This may also causes for the above error message. With the experience of extra expect_call case, I have taken the stack trace or back trace using GDB, and I found that for one expect call I used WillOnce. So changed to WillRepeatedly. It got solved.

After my analysis and contacting with our UT team, I came to know that the possible reason for this problem is that calling extra EXPECT_CALL for the unused functions.

C Program to create threads!!

Below is the simple C program to create the thread.

#include<stdio.h>
#include<pthread.h>

void *print_data(void *str)
{
    char *msg = (char *)str;
    printf("given message is '%s'\n",msg);
}
main()
{
    pthread_t th1,th2;
    int ret1,ret2;
    char msg1[]="this is first message";
    char msg2[]="this is second  message";

    ret1 = pthread_create(&th1,NULL, print_data,(void *)msg1);
    ret2 = pthread_create(&th2,NULL, print_data,(void *)msg2);

    printf("th1 return value is %d\n",ret1);
    printf("th2 return value is %d\n",ret2);

    pthread_join(th1,NULL);
    pthread_join(th2,NULL);
}

loop in linked list C program!!

Below is the C  program for finding the loop in a linked list 

#include<stdio.h>
#include<stdlib.h>
struct node
{
    int info;
    struct node *next;
};

typedef struct node Node;

Node* append(Node *h, int info)
{
    Node *tempHead=h;
    Node *newNode = (Node*)malloc(sizeof(Node));
    newNode->info = info;
    newNode->next = NULL;
    if(tempHead == NULL) // if the list has zero elements. make new node as a head
    {
        h=newNode;
    }
    else    if(tempHead->next==NULL)  // if the list is having only one node
    {
        tempHead->next = newNode;
    }
    else
    {
        Node *tempNode = h;
// if the list has more than one node, so moving to the last node
        while(tempNode->next != NULL)  
        {
            tempNode = tempNode->next;
        }
        tempNode->next = newNode; // appending the new node at the end
    }
   // this is for making the list circular/loop
    if(info == 101) 
    newNode->next = h;
    return h;
}


/*****************************************************************************
for displaying the nodes in the list. 
Dont call this function if the list contains loop. 
if you call you wont get the end, becaue there is no NULL in the list
*****************************************************************************/
void display(Node *h)
{
    Node *temp = h;
    while (temp->next!=NULL)
    {
        printf("%d->",temp->info);
        temp = temp->next;
    }
    printf("%d\n",temp->info);
}

/*************************************************************************************
let me explain the concept first. for finding the loop in a single linked list,  
need to take two temparty nodes tempOne and tempTwo, move temOne node one level 
and move tempTwo two levels(tempTwo->next->next) until tempTwo/tempOne 
reaches NULL, if the list contains loop somewhere, these two nodes must be met/same, 
if not met/same, there is no loop in the list
***************************************************************************************/

int loop(Node *head)
{
    Node *tempOne = head;
    Node *tempTwo = head;
    while( tempTwo->next!=NULL )
    {
        tempTwo = tempTwo->next;  // one  move
        if(tempTwo->next!=NULL)
        {
           // if second move is equal to tempOne then there is loop
            if(tempTwo->next==tempOne) 
                return 1;
            else
            tempTwo=tempTwo->next;   // second move
        }

        tempOne = tempOne->next;  // one move
    }
    return 0;
}
main()
{
    Node *head = NULL;
    int i;
    for (i=1;i<=10;i++)
    {
        head = append(head,i*10);
    }
    display(head);
    head = append(head,101); // this element for making loop in the list
    i=loop(head);
    if(i)
        printf("loop found in the list\n");
    else
        printf("no loop in the list\n");
}