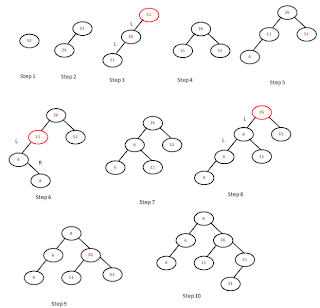
Lets constrcut the AVL tree with numbers 51, 26, 11, 6, 8, 4, 31, 21, 9, 16. AVL tree is a balanced Binary search tree. So to construct AVL tree, we need to follow below steps
51, 26, 11, 6, 8, 4, 31, 21, 9, 16.
- insert the new element in such a way that if the element is less than the current node go left and if the element is greater than go right.
- Check for the balance at each node after insertion (diff between left subtree and right subtree should be atmost one)
51, 26, 11, 6, 8, 4, 31, 21, 9, 16.
- In step1 the tree is empty , so 51 is the first node, in step2 26 is inserted as a left child to the root node 51 and the tree is balanced.
- In step3 11 is added as a left child to the node 26, becaus of this root node 51 is un-balanced, as it is shown in the image as red circle. We need to do the left left rotation which is a single rotation.
- After the rotation, tree is balanced as shown in step4.
- in step5 we are inserting 6 into the tree and which is as a left child to the node value 11.
- in step6 we are inserting 8 into the tree and which is as a right child to the node value 6, because of this tree is un-balanced at node value 11 which is marked as red circle in the image.
- for balancing the node we need to do right-left rotation which is a double rotation.
- After the rotation, the tree is balanced and it is like as shown in step7.
- In step8 we are inserting 4 into the tree and which is as a left child to node value 6. Becaus of this insertion, the tree is un-balanced at node value 26, and we need to do the left-left rotation as we did it earlier.
- After the rotation the tree is like shown in step9. After that we need to insert 31 into the tree and which is as a left child to the node value 51 as shown in step10. And the tree is balanced.
- In step11 we are inserted 21 into the tree whihc is as a right child to the node value 11. In step12 we inserted 9 as a left child to the node value 11. And the tree is balanced.
- in step13, becaus of inserting 16 as a left child to the node value 21, the tree is un-balanced at node value 8.
- We need to do the left right rotation which is a double rotation. And the resultant tree is as shown in step14.


4 comments:
Very useful information on Data Structures, definitely it helps us to protect our site from copied content, if you are Looking for software courses?
cloud computing training in chennai
Hadoop Training in Chennai
Selenium Training in Chennai
Digital Marketing Course in Chennai
JAVA Training in Chennai
German Classes in chennai
Loadrunner Training in Chennai
performance testing training in chennai
Home of Kali Linux, an Advanced Penetration Testing Linux distribution used for Penetration Testing, Ethical Hacking and network security assessments. Online Wifi Password Hack
Pandora One Premium Mod Apk is the right choice for you ,you wanna stream and enjoy high quality music so download.Pandora APK Download
Do students want to engage with higher education management through social media? Many don't, but some do. Love Husband Good Morning Images
Post a Comment