Here we will learn how to construct a binary tree from a given traversals Inorder and Preorder/Postorder. Traversal means visiting each node in the tree in some specified order like preorder, postorder or inorder. We will get the traversal from the given binary tree. And we can also construct binary tree from the given traversals. We see how to construct the tree from traversals.
Construct Binary Tree from Traversals: To construct binary tree we need
Inorder: DBEAFCG
PreOrder: ABDECFG
As mentioned above, to construct a tree we need at least two traversals in that one must be Inorder and another must be either Preorder or Postorder. Inorder is for finding left and right child nodes and pre or post order is for finding the root node.
If the preorder is given, first element in the preoder is root node. And if the postorder is given last element is the root node. After finding the root node, go to Inorder and find the root node in the inorder and left elements of the root node are left childs and right elements of the root node are right childs. Repeat this process for all elements.
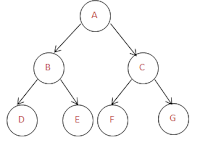
Step1: From Preorder first eleement is the root node.So here it is 'A'. If you see 'A' in in order and left of the A are left childs here DBE and right childs of A are FCG.
PreOrder: ABDECFG
Inorder: DBE A FCG
Step 2: we will repeat the step1 for two sub elements BDE and CFG. from preorder first element is root node, here B and C are root nodes and from the Inorder D is the left child and E is the right child for B. Similarly F is the left child and G is the right child for C.
PreOrder: A BDE CFG
Inorder: DBE A FCG
Lets take another example with Inorder and Postorder.
Postorder: DHIEBJFGCA
Inorder: DBHEIAFJCG
Step1: From postorder last element is the root node, So here A is the root node and from from inorder we will find the left and right sub elements.
Postorder: DHIEB JFGC A
Inorder: DBHEI A FJCG
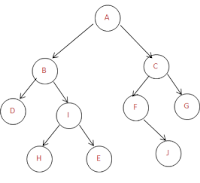
Step2: we will repeat the step1 for left and right sub elements. From Inorder left elements are 5 and right elements are 4. we will split the Postorder like that and take the root nodes as B and C.
Postorder: DHIEB JFGC A
Inorder: D B HEI A FJ C G
Step3: For root node B left element is one(D) and right elements are three(HIE) and for C left element are two(JF) and right element is one(G).
Postorder: D HIE B JF G C A
Inorder: D B HEI A FJ C G
Construct Binary Tree from Traversals: To construct binary tree we need
- Inorder traversal data and
- Postorder or Preorder traversal data
Inorder: DBEAFCG
PreOrder: ABDECFG
As mentioned above, to construct a tree we need at least two traversals in that one must be Inorder and another must be either Preorder or Postorder. Inorder is for finding left and right child nodes and pre or post order is for finding the root node.
If the preorder is given, first element in the preoder is root node. And if the postorder is given last element is the root node. After finding the root node, go to Inorder and find the root node in the inorder and left elements of the root node are left childs and right elements of the root node are right childs. Repeat this process for all elements.
Step1: From Preorder first eleement is the root node.So here it is 'A'. If you see 'A' in in order and left of the A are left childs here DBE and right childs of A are FCG.
 |
| Step1 tree |
Inorder: DBE A FCG
Step 2: we will repeat the step1 for two sub elements BDE and CFG. from preorder first element is root node, here B and C are root nodes and from the Inorder D is the left child and E is the right child for B. Similarly F is the left child and G is the right child for C.
PreOrder: A BDE CFG
 |
| Step2 Tree |
Lets take another example with Inorder and Postorder.
Postorder: DHIEBJFGCA
Inorder: DBHEIAFJCG
 |
| Step1 Binary tree |
Postorder: DHIEB JFGC A
Inorder: DBHEI A FJCG
 |
| Step2 Binary Tree |
Postorder: DHIEB JFGC A
Inorder: D B HEI A FJ C G
 |
| Final Binary tree |
Postorder: D HIE B JF G C A
Inorder: D B HEI A FJ C G

No comments:
Post a Comment